Home > Scuola > Disegno > Disegnare con i quadretti > Disegni sul piano cartesiano
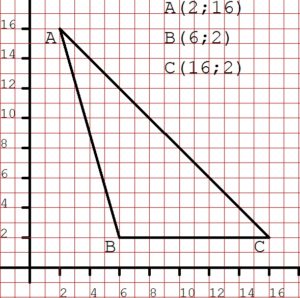
Il piano cartesiano è un sistema di riferimento costituito da due rette orientate, perpendicolari tra di loro, una disposta orizzontalmente (ascissa o asse x), una disposta verticalmente (ordinata o asse y). Ascissa e ordinata si intersecano in un punto detto “origine”. In questo sistema di riferimento viene fissata anche un’unità di misura. Ogni punto sul piano cartesiano viene individuato da due coordinate, la prima indica la distanza del punto dall’asse y (e quindi si misura lungo l’asse x), la seconda indica la distanza del punto dall’asse x (e quindi si misura lungo l’asse y), come nel gioco della battaglia navale. Le coordinate di un punto si indicano tra parentesi, separate da un punto e virgola. Nel disegno sotto vediamo rappresentati tre punti sul piano cartesiano, in alto a destra sono riportate le coordinate dei tre punti, inoltre vediamo raffigurato anche il triangolo che i tre punti formano.
Su un foglio da disegno quadrettato possiamo disegnare anche due piani cartesiani, come mostra la figura sotto:
Per ingrandire l’immagine potete cliccare qui. Cliccando su questo link si accede ad un’immagine come quella sopra ma in alta definizione ed in formato bitmap, che è più adatta per creare dei disegni con Paint rispetto ad un’immagine in formato jpeg.
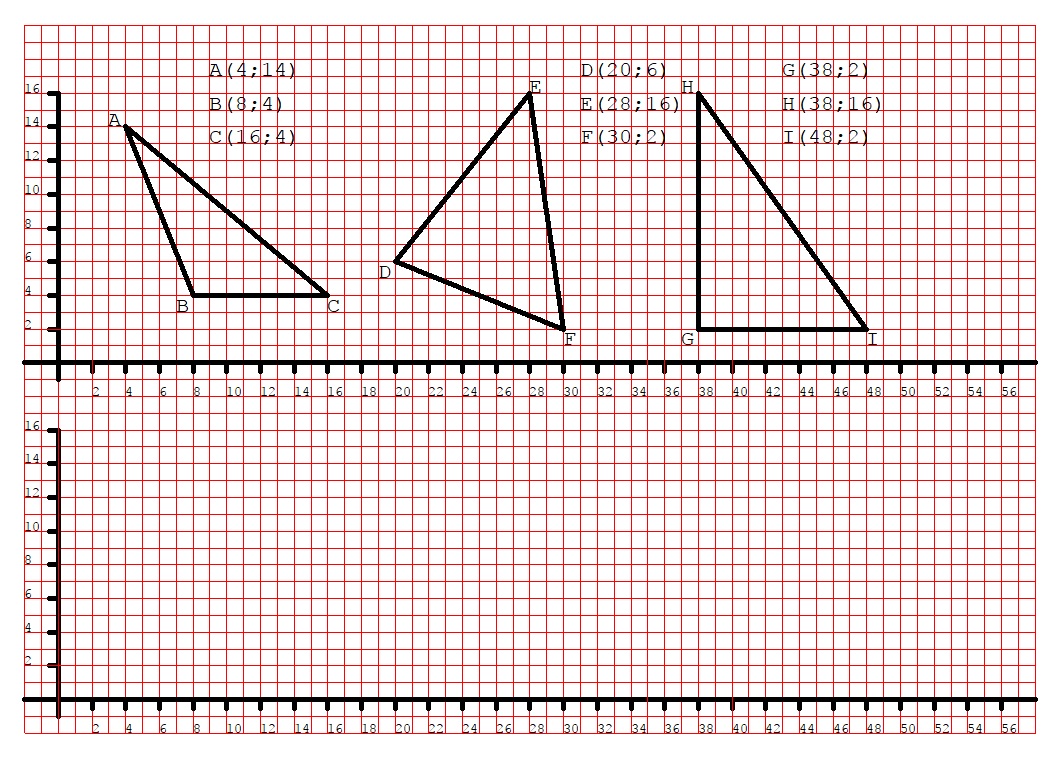
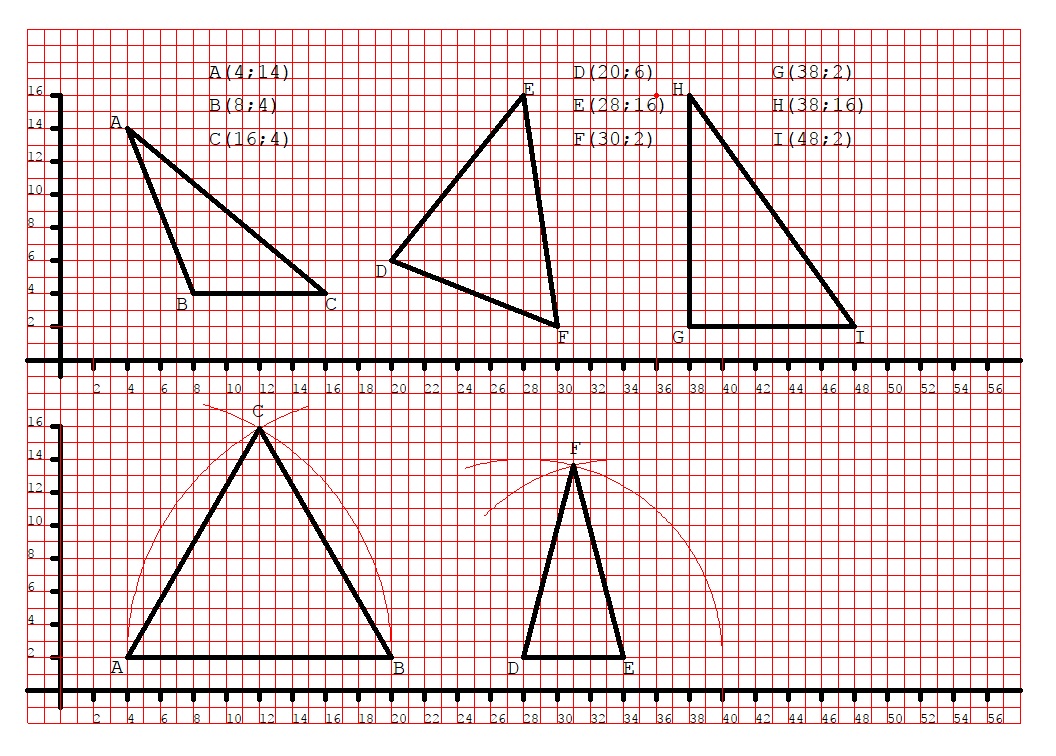
Dopo aver predisposto due piani cartesiani sul foglio, come illustrato nella figura sopra, nel primo dei due piani individuare i punti A (4;14), B (8;4) e C (16;4) e congiungerli: che tipo di triangolo si ottiene?
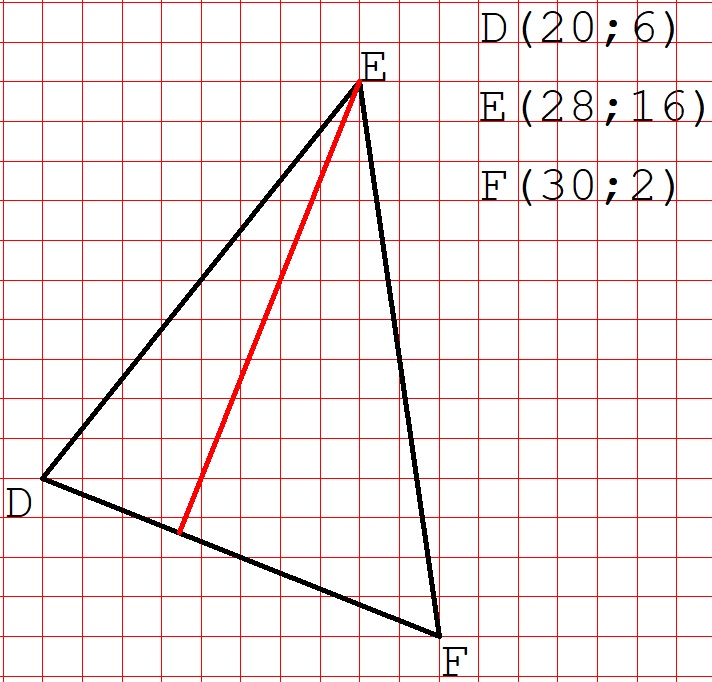
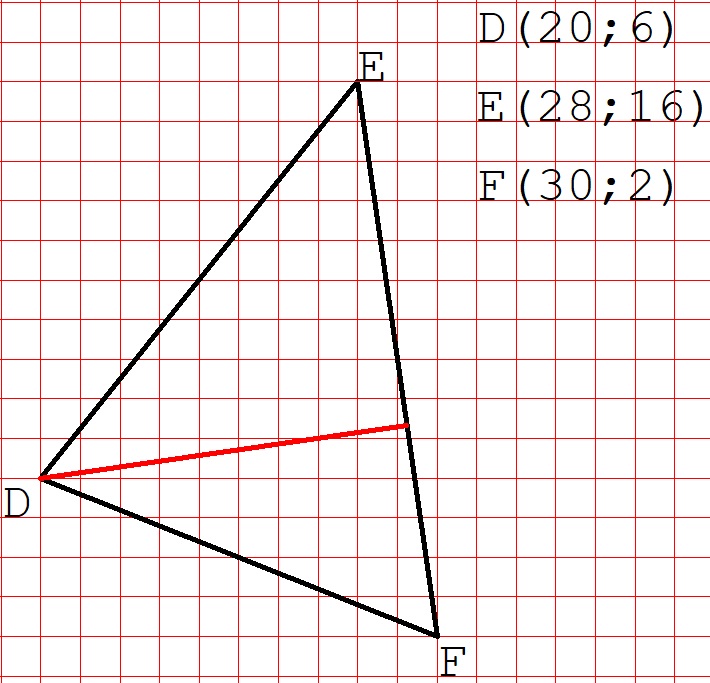
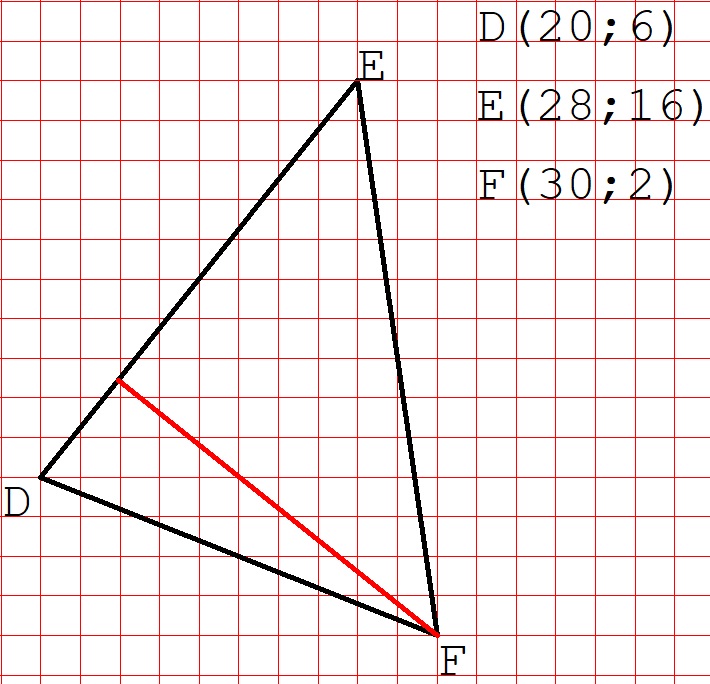
Ora invece individuate i punti D (20;6), E (28;16) e F (30;2) e congiungeteli: che tipo di triangolo ottenete?
Infine individuate i punti G (38;2), H (38;16) e I (48;2) e congiungeteli: che tipo di triangolo ottenete?
Il triangolo DEF è un triangolo scaleno ed è un triangolo acutangolo. Come tutti i triangoli possiede 3 altezze: una che parte dal vertice E ed arriva perpendicolarmente al lato DF.
Un’altra altezza di questo triangolo è quella che parte dal vertice D ed arriva perpendicolare al lato EF:
L’ultima altezza del triangolo DEF parte dal vertice F e arriva perpendicolare al lato DE:
Per trovare le altezze in un triangolo possiamo farci guidare da una squadra:
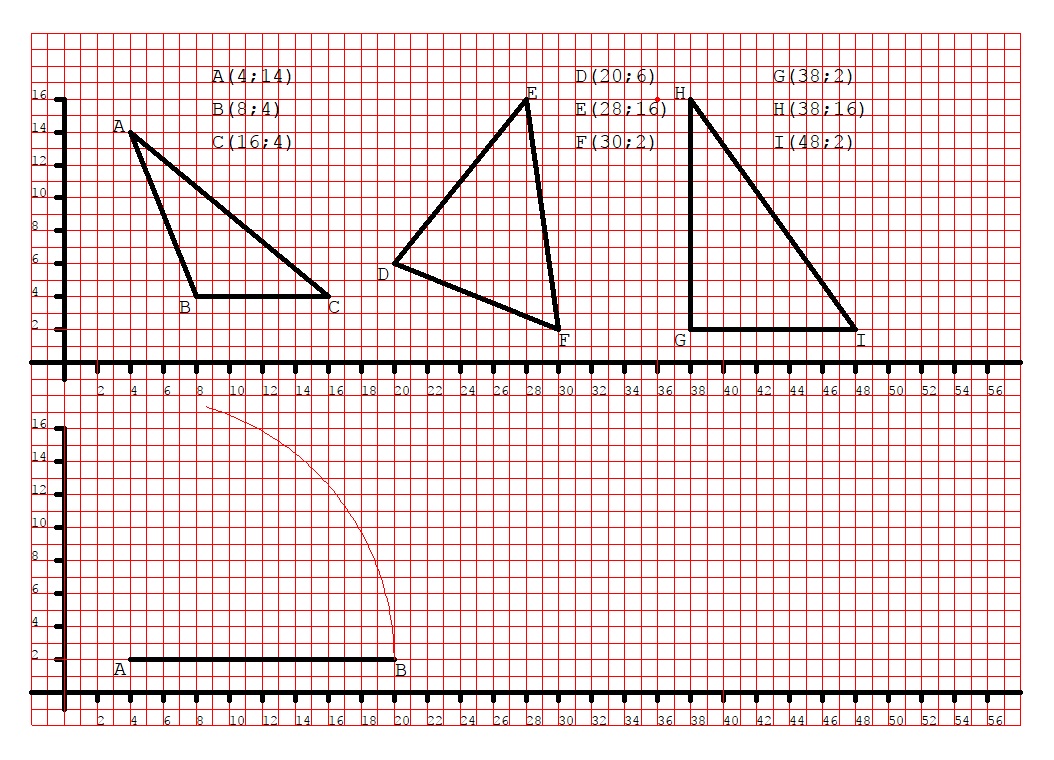
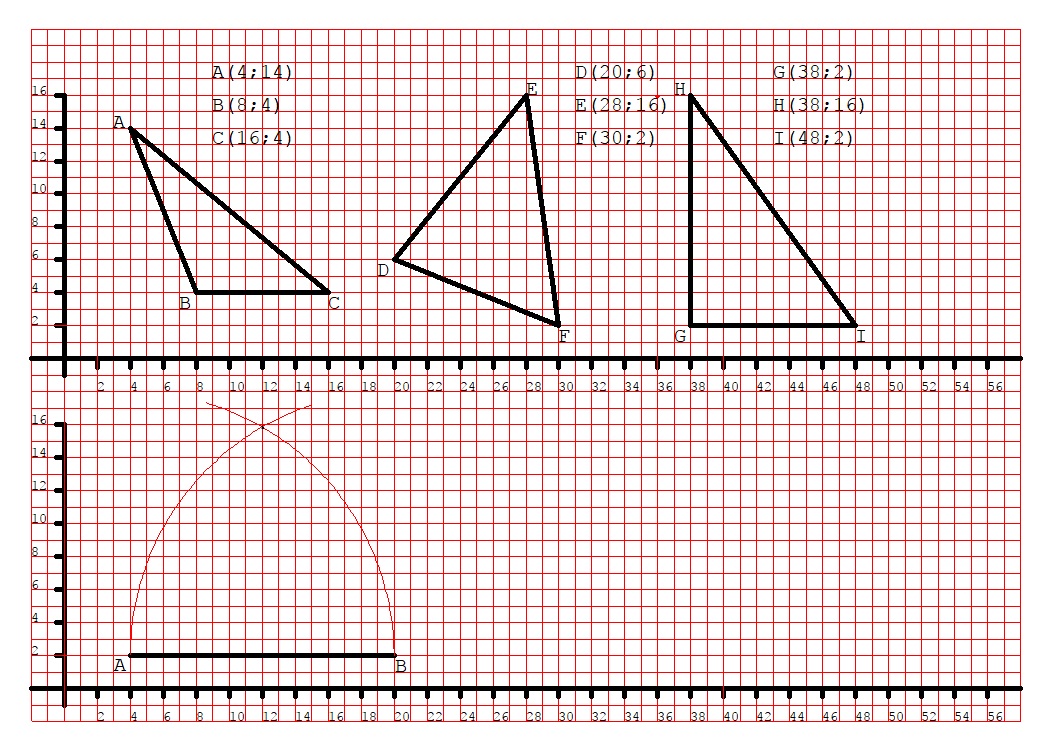
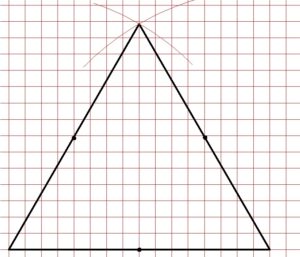
Sul piano cartesiano che abbiamo disegnato nella seconda parte del foglio tracciamo il segmento AB con A(4;2) e B(20;2). Dato un segmento qualsiasi, nel nostro caso dato il segmento AB, per tracciare un triangolo equilatero avente il lato pari al segmento dato si prende il compasso, lo si punta in A, lo si apre tanto quanto è lungo il segmento AB e si traccia un arco.
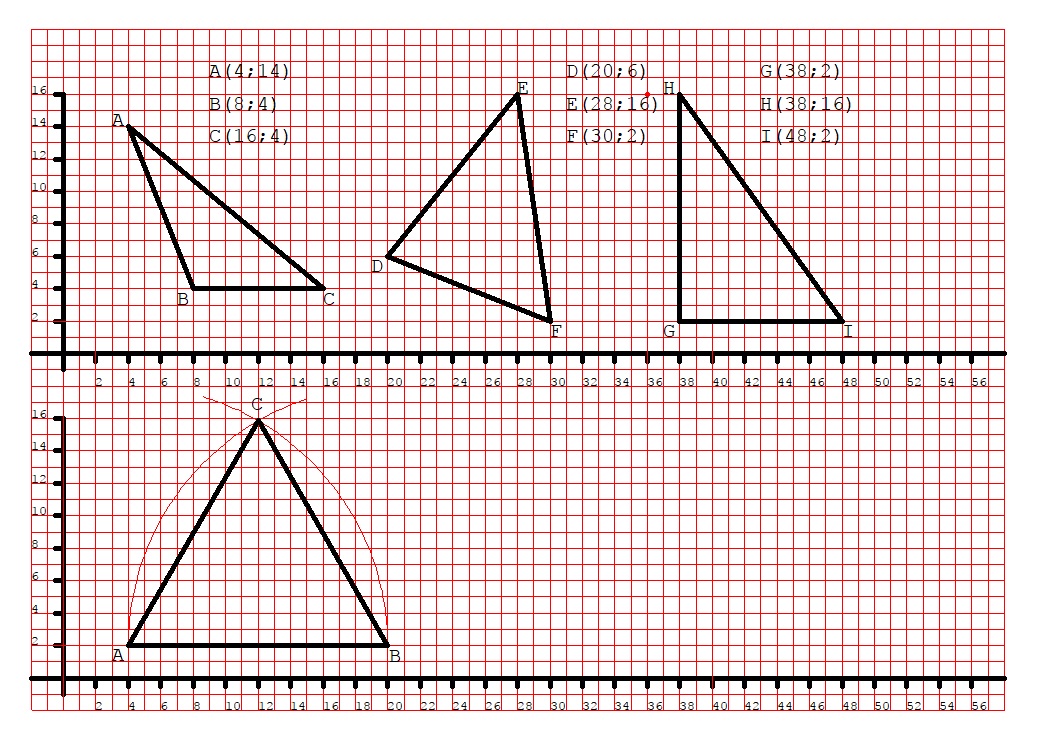
Poi si punta il compasso in B, mantenendo sempre la stessa apertura, e si traccia un secondo arco che intersecherà il primo arco in un punto che chiameremo C:
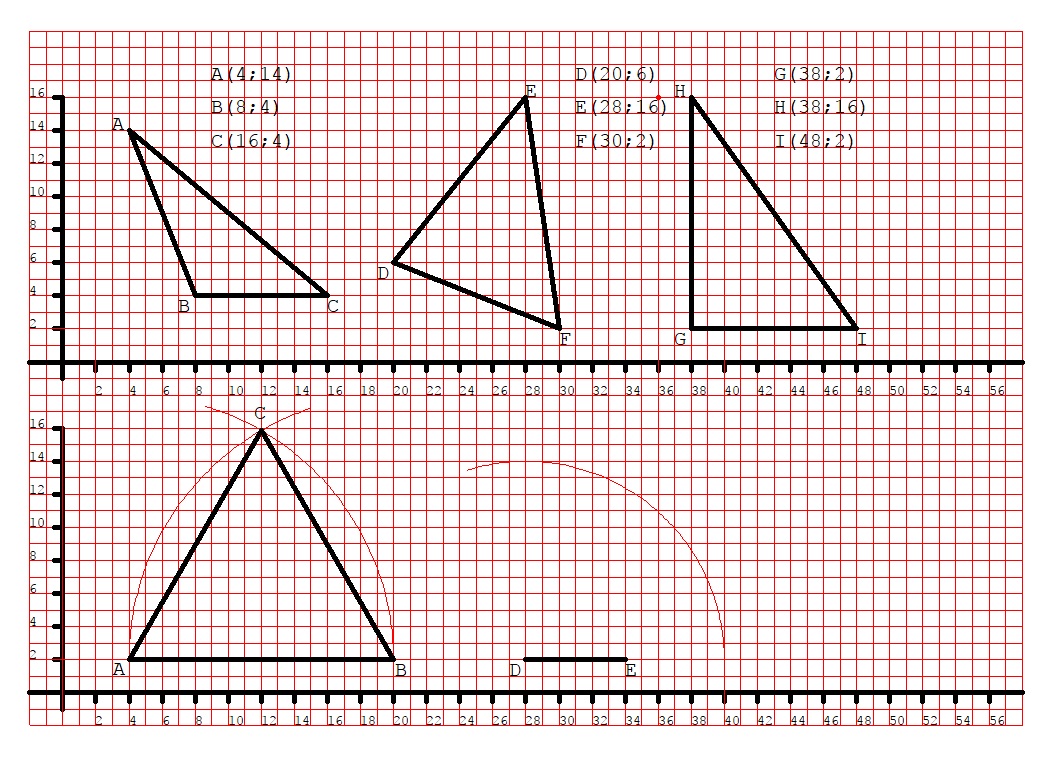
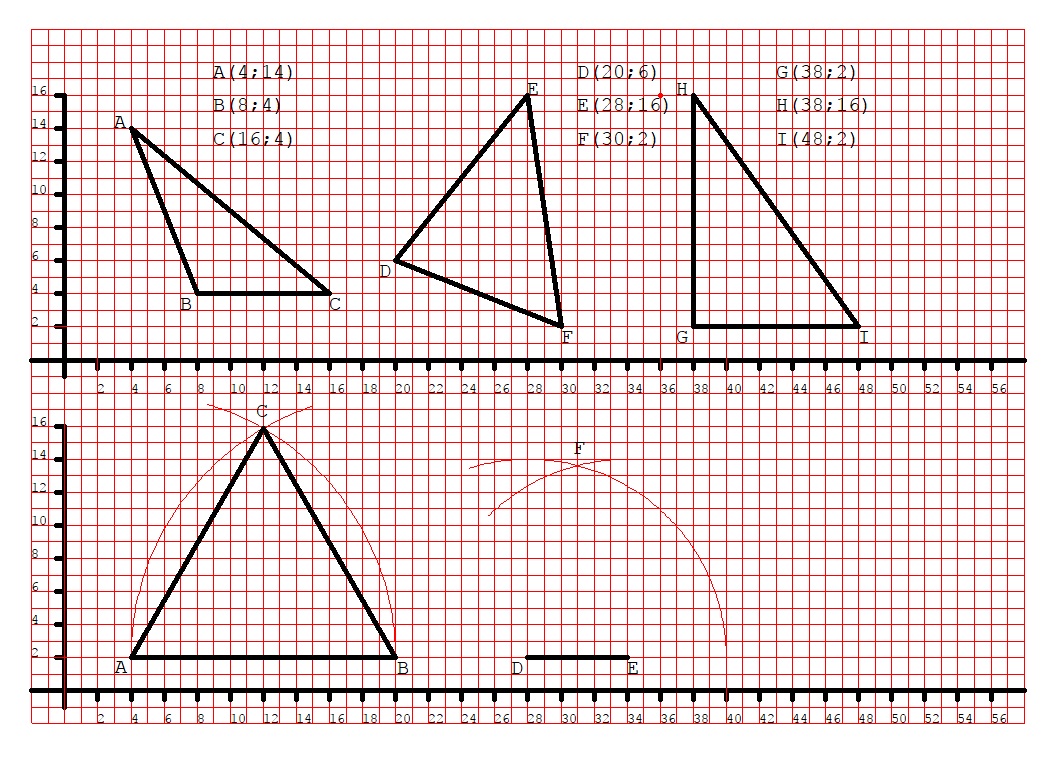
Infine, sempre sul piano cartesiano che abbiamo disegnato nella seconda parte del foglio, tracciamo il segmento DE con D(28;2) ed E(34;2). Ipotizziamo ora di dover tracciare un triangolo isoscele, avente il lato disuguale lungo 6 quadretti (proprio come il segmento DE) e gli altri due lati lunghi 12 quadretti, per disegnarlo partiamo dal segmento DE che abbiamo appena tracciato e che costituisce il nostro lato di 6 quadretti. Per tracciare gli altri due lati ci facciamo aiutare dal compasso: lo si apre tanto quanto saranno lunghi i due lati che dobbiamo disegnare, cioè 12 quadretti. Poi lo si punta in D e si traccia un arco.
Poi si punta il compasso in E, mantenendo sempre la stessa apertura, e si traccia un secondo arco che intersecherà il primo arco in un punto che chiameremo F:
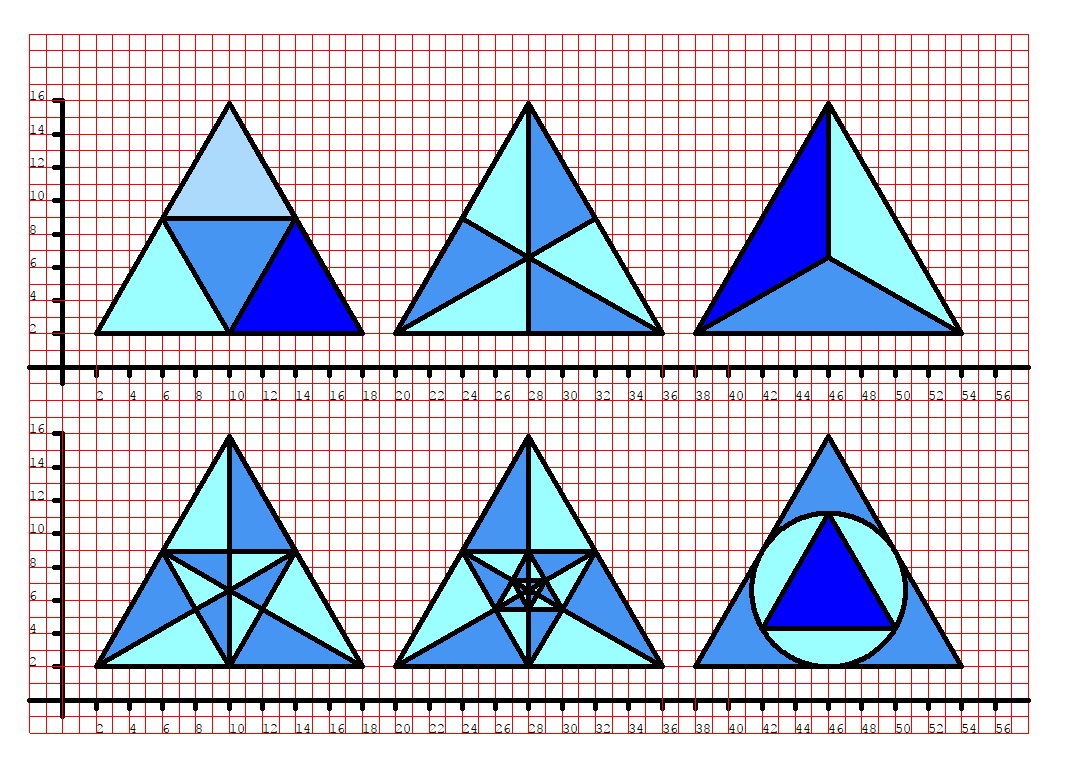
Ecco un esempio di alcune semplici decorazioni colorate su sei triangoli equilateri costruiti sul piano cartesiano, il lato di ognuno di questi triangoli equilateri è di 16 quadretti:
Per disegnare questi triangoli utilizziamo il compasso, con un’apertura di 16 quadretti, inoltre dobbiamo individuare il punto medio di tutti i lati:
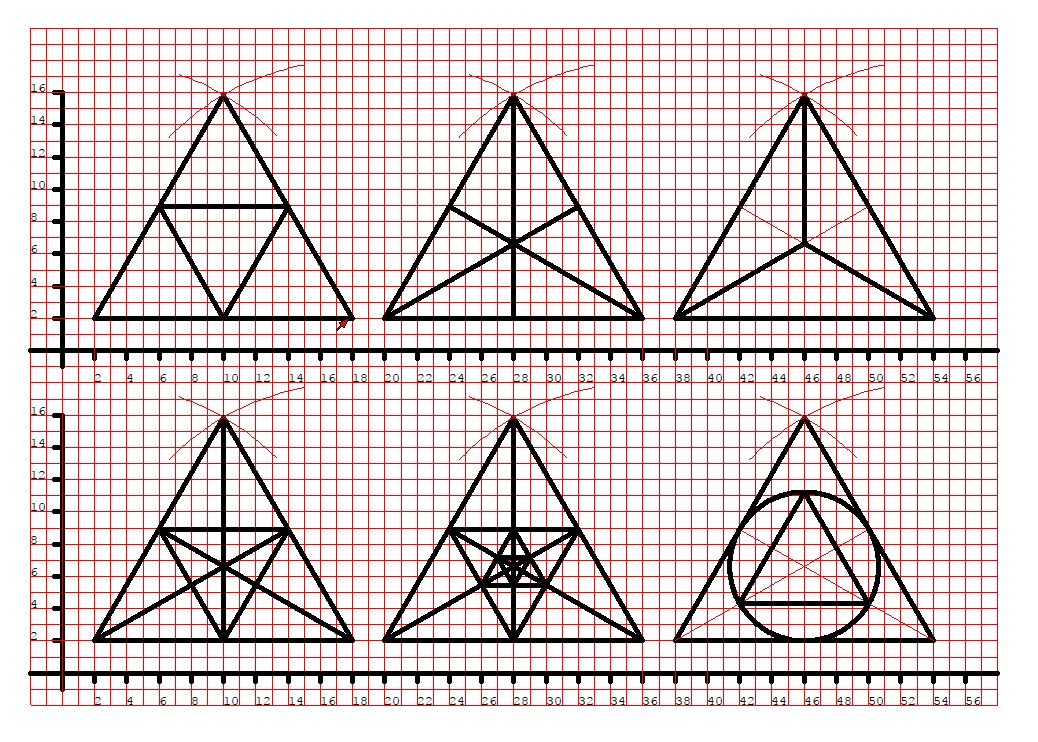
Per ottenere il primo triangolo sarà sufficiente congiungere i tre punti medi, per ottenere il secondo triangolo bisognerà tracciare le tre mediane del triangolo (la mediana è un segmento che unisce il punto medio di un lato con il vertice opposto). Per ottenere il terzo triangolo, le mediane dovranno essere prima tracciate con la matita 2H, poi solo una parte di queste tre linee dovrà essere ripassata con la matita HB:
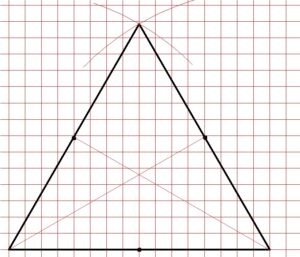
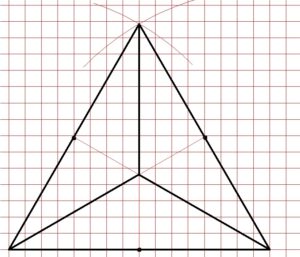
Il quarto triangolo si ottiene a partire dal primo ed aggiungendo le mediane. Il quinto triangolo si ottiene a partire dal quarto triangolo e congiungendo i punti medi del triangolo interno (i punti medi tra l’altro sono indicati dalle mediane del triangolo più grande, che per questioni di geometria saranno anche le mediane di tutti gli altri triangoli che disegneremo all’interno), comparirà così un triangolo interno più piccolo, all’interno del quale ne otterremo uno ancora più piccolo congiungendo i punti medi (volendo potremmo andare avanti così all’infinito…)
Il sesto triangolo invece si ottiene tracciando le mediane del triangolo con la matita 2H. Le tre mediane di un triangolo equilatero coincidono con le bisettrici, ed il punto di incontro delle bisettrici di un triangolo si chiama INCENTRO. Puntando il compasso nell’incentro ed aprendolo tanto quanto la distanza tra l’incentro ed il punto medio di uno qualsiasi dei tre lati di questo triangolo equilatero otteniamo la circonferenza INSCRITTA nel nostro triangolo equilatero. Infine, congiungendo ognuno dei punti in cui le tre mediane-bisettrici incontrano la circonferenza inscritta, si ottiene il triangolo più interno.

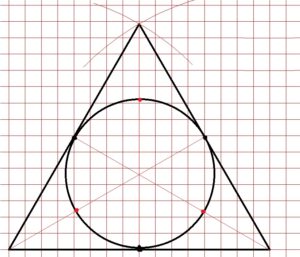
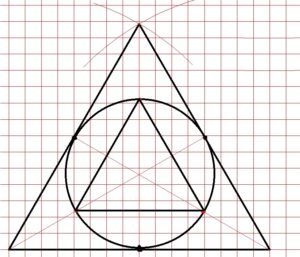
Ecco un altro esempio di alcune semplici decorazioni colorate su sei triangoli equilateri costruiti sul piano cartesiano, il lato di ognuno di questi triangoli equilateri è di 16 quadretti: